La sezione aurea è un numero irrazionale, di solito indicato con la lettera greca phi, pari a 1,61803... Si tratta di un numero irrazionale legato a numerose costruzioni geometriche. La sua particolarità è dovuta al fatto che compare negli ambiti più inaspettati: in botanica, in architettura, in biologia. In ogni caso è sempre sinonimo di armonia e di bellezza. Per maggiori particolari rimando al bel libro La sezione aurea di Mario Livio da cui ho tratto l´ispirazione per i seguenti frattali.
La sezione aurea è anche legata al pentagono regolare in quanto la diagonale ed il lato del poligono hanno come rapporto proprio phi (e quindi risultano incommensurabili). In effetti, più in generale, in un triangolo isoscele con gli angoli alla base pari a 72° il lato e la base hanno come rapporto phi. Si dice allora che il triangolo è aureo.
Ogni pentagono contiene un pentagramma, ovvero la stella a cinque punte che si ottiene collegando tutti i vertici del pentagono tramite diagonali. Nella figura che segue il pentagono con il relativo pentagramma.
La forma del pentagramma è riscontrabile molto spesso in natura, come ad esempio in alcune piante grasse.

Vediamo come costruire un merletto di Koch legato alla sezione aurea. Chiameremo il frattale Merletto aureo.
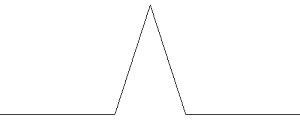
L'idea è semplice. Sostituiamo il segmento iniziale con quattro segmenti di uguale ampiezza in modo tale che il triangolo isoscele che si venga a formare sia aureo. Si tratta infatti di un triangolo isoscele con gli angoli alla base pari a 72°. Tralascio volutamente i particolari tecnici della costruzione che in ogni caso è analoga a quella del Merletto di Koch.
|
Passo 0
|
Passo 1
|
 |
 |
|
Passo 2
|
Passo 3
|
 |
 |
La particolarità del frattale finale sta nel fatto che tutti i triangoli isosceli che si vengono a formare sono tutti aurei. Nel Merletto di Koch classico invece tutti i triangoli che si venivano a formare erano equilateri.

Il fattore di omotetia k legato alla costruzione di questo frattale è 1/2,6180... ovvero 1/phi2. La dimensione del frattale sarà pari a : D=log 4 / log (phi2) = 1,44... Si tratta di un valore superiore a quello del Merletto di Koch in quanto il merletto aureo "riempie maggiormente" il piano.
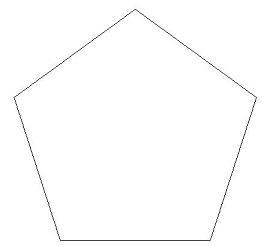
Costruiamo lo stesso frattale sui lati di un pentagono regolare. Il frattale viene costruito dentro il pentagono.
|
Passo 0
|
Passo 1
|
 |
 |
|
Passo 2
|
Passo 3
|
 |
 |
Il risultato finale è il seguente:

La costruzione è analoga a quella del Fiocco di neve di Koch. La differenza sta nel fatto che il pentagono frattale è un frattale legato al pentagono regolare e che quindi ne eredita le proprietÓ geometriche mentre il Fiocco di neve di Koch Ŕ legato al triangolo equilatero ed eredita le proprietÓ di questa figura. Questo implica che da una parte avremo angoli di 108°, 72° e 36°, dall'altra angoli di 120° e 60°.
Costruendo il merletto aureo sui lati del pentagramma invece che sui lati del pentagono, otteniamo il seguente frattale, a forma di stella. Caratteristica particolare di questo frattale è quella di contenere infinite copie del pentagono aureo tutte perfettamente incastrate fra di loro.

Nella seguente figura le copie del pentagono frattale sono messe in evidenza con colori diversi. In questo modo è possibile osservare che sono presenti i vari passi della costruzione del pentagono frattale. Le parti in grigio corrispondono al passo 0, quelle in rosa al passo 1, quelle in giallo al passo 2 e così di seguito. Si tratta di un vero e proprio riassunto della costruzione del pentagono frattale.

Nel sito sono presenti anche altri frattali legati al pentagono e quindi anche alla sezione aurea: i fiocchi di neve pentagonali.