La spirale è quella curva piana che ha la proprietà di avvolgersi in infiniti giri intorno ad un punto. È una struttura molto diffusa in natura: dai cicloni alle galassie, dalle corna d'alcuni animali (come i montoni) fino alle conchiglie, dal moto dei cicloni alla molecola del DNA, dai fiori di girasole fino alle zanne degli elefanti.
Un tipo particolare di spirale è la spirale logaritmica.
L'equazione in coordinate polari è la seguente: 
dove 
è l'angolo costante formato dal raggio e dalla tangente.
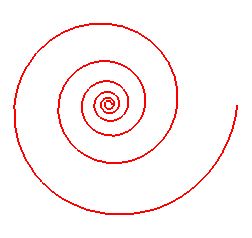
La spirale logaritmica si può pensare ottenuta anche nel seguente modo. Consideriamo una semiretta che ruota uniformemente intorno ad un suo estremo ed un punto che si muove lungo questa semiretta con velocità che aumenta man mano che il punto si allontana dall'estremo fissato. Il punto traccia una curva che è appunto una spirale logaritmica.
Il matematico Jacques Bernoulli (1654-1705) fu un grande studioso di curve e rimase particolarmente affascinato dalla spirale logaritmica. Ne dimostrò molte proprietà inedite e volle che fosse incisa sulla sua tomba accompagnata dal motto Eadem mutata resurgo (Trasformata nella dimensione, rinasco sempre uguale).
Infatti, osservando la figura si nota che la spirale logaritmica prosegue indefinitamente sia verso l'interno sia verso l'esterno: la curva si avvolge intorno al punto centrale senza mai raggiungerlo. Il centro della spirale logaritmica, osservato con un qualsiasi ingrandimento, appare costantemente come una spirale infinita.
In conclusione la spirale logaritmica è una figura autosimile e di conseguenza può essere considerata un frattale. Per la precisione si tratta di un frattale con condensing.
La spirale logartmica può essere ottenuta considerando come figura di partenza un punto posto ad una certa distanza dall'origine ed applicando a questo punto una similitudine. Nella figura che segue il punto di partenza è evidenziato in rosso. La figura ottenuta è una spirale logaritmica.
La similitudine applicata è ottenuta componendo una omotetia con rapporto di omotetia K minore di 1 ed una rotazione. Naturalmente il risultato ottenuto cambia al variare dei coefficienti.
Considerando come figura di partenza una circonferenza si ottengono figure simili ad una conchiglia.
Per maggiori particolari sulle curve consiglio il libro Le Curve celebri di Cresci. Invece per conoscere tutte le infinite applicazioni della spirale in natura consiglio il testo Che forma ha un fiocco di neve di Stewart.
Altri esempi di spirali nel sito si possono trovare nella sezione dedicata alla composizione di trasformazioni geometriche.
Inoltre due pagine sono dedicate alle spirali nelle piante grasse: una con le foto più leggere, un'altra con foto più grandi.
In un'altra pagina del sito dei frattali la cui forma ricorda le spirali.