Cerchiamo ora di risolvere il seguente problema, molto importante nello studio della geometria frattale.
Come si possono ricavare le trasformazioni che generano un certo frattale a partire dal risultato finale ovvero dall'attrattore?
La questione è stata affrontata e risolta da Barnsley tramite il cosiddetto Teorema del Collage . Qui mi limiterò ad illustrare il procedimento da un punto di vista molto elementare presentando alcuni esempi. Al testo di Barnsley rimando per una trattazione più completa ed esauriente dell'argomento.
Consideriamo ad esempio il Triangolo di Sierpinski (fig. 1). Poiché tale figura è un frattale, ha una struttura autosimile (o autosomigliante). Questo vuol dire che contiene tantissime copie di se stesso. Cerchiamo il minimo numero di copie del frattale che mi permette di comprenderlo tutto. Devono essere ricoperti tutti i punti del frattale e ciascun punto deve essere scelto una sola volta. In altre parole, è come se dovessimo ricoprire il frattale con tante copie del frattale stesso, in modo tale che ciascun punto sia coperto una sola volta. Le copie sono 3 e sono evidenziate nella figura seguente (fig. 2).
|
(fig. 1) |
(fig. 2) |
Ad essere precisi, esistono anche 9 copie del frattale o anche 27 copie che mi permettono di ricoprirlo tutto, ma abbiamo scelto per semplicità il numero minore di copie, ovvero 3.
Ora cerchiamo le trasformazioni geometriche che applicate al frattale, lo trasformano nelle tre copie che abbiamo individuato. Abbiamo tre copie e di conseguenza cerchiamo tre trasformazioni. Si tratta di tre omotetie di ragione 1/2 poiché la figura diventa la metà di quella iniziale. Poi occorrerà comporle con opportune traslazioni. Per ottenere un'espressione analitica delle trasformazioni, occorre fissare un opportuno sistema di riferimento. Per semplicità supponiamo che il frattale sia costruito dentro il quadrato di lato unitario e l'origine sia posta nell'angolo a sinistra in basso.
Per ottenere il triangolo di Sierpinski basta usare le seguenti tre trasformazioni:
T1:
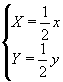 ;
;
T2:
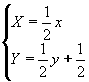 ;
;
T3:
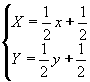 .
.
L'origine del sistema di riferimento è posto nel vertice in basso a sinistra del quadrato di partenza. Nota che è T 1 un'omotetia di ragione 1/2, T2 è un'omotetia di ragione 1/2 composta con una traslazione secondo il vettore (0, 1/2), T3 è un'omotetia di ragione 1/2 composta con una traslazione secondo il vettore (1/2, 1/2).
Naturalmente, più il frattale sarà complesso, maggiore risulterà il numero delle trasformazioni necessarie.
Consideriamo ora il Merletto di Koch.
Anche in questo caso determiniamo il numero di copie che ci permette di ricoprire tutto il frattale senza sovrapposizioni. E' facile verificare che il numero delle le copie in questo caso è 4 e tale sarà anche il numero delle trasformazioni geometriche che generano il frattale (fig. 4). (Sia chiaro che sono possibili anche altre scelte. Questa è la costruzione classica di questo frattale.)
Le trasformazioni sono le seguenti:
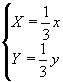 ;
T
2
:
;
T
2
:
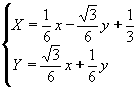 ;
T
3
:
;
T
3
:
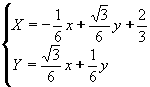 ;
T
4
:
;
T
4
:
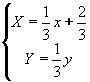 ;
;
L'origine del sistema di riferimento è posto nel vertice in basso a sinistra della figura di partenza. Nota che è T 1 un'omotetia di ragione 1/3, T 2 è un'omotetia di ragione 1/3 composta con una rotazione di 60 gradi in senso antiorario ed una traslazione secondo il vettore (1/3,0). T 3 è un'omotetia di ragione 1/3 composta con una rotazione ed una traslazione secondo il vettore (2/3, 0). Infine T 4 è un'omotetia di ragione 1/3 composta con una traslazione secondo il vettore (2/3,0).
Osserva ora un altro frattale: la Scatola frattale.
Cerca di determinare da solo le trasformazioni che generano il frattale, procedendo come negli esempi precedenti. Poi controlla le soluzione proposta .