Un frattale, molto simile per costruzione al l' albero di Barnsley è l'albero aureo.
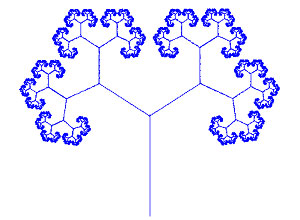
Nell'albero di Barnsley in figura per ottenere la chioma dell'albero si usano due similitudini con coefficiente di omotetia k=0,6 ed angolo di rotazione pari a 60°. Il risultato può variare leggermente a seconda dei coefficienti usati.
Si potrebbe voler ottimizzare il coefficiente di omotetia in modo da rendere l'albero il più frondoso possibile, senza però sovrapposizioni delle foglie. Nel mondo vegetale, il problema della disposizione delle foglie nel modo più efficiente possibile è risolto ponendo le foglie lungo delle spirali. Queste spirali sono legate alla successione di Fibonacci e quindi alla sezione aurea. Di conseguenza non stupisce scoprire che il coefficiente di omotetia necessario è pari a k=0,618... ovvero 1/phi dove phi=1,618... è la sezione aurea. La dimostrazione rigorosa è contenuta nel libro La sezione aurea di Mario Livio.
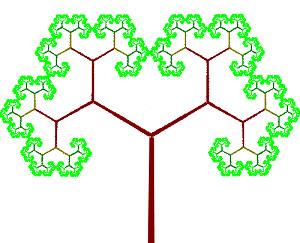
In questo modo si ottiene il seguente albero aureo. Per ottenere un risultato più naturale possibile, è stata usata la tecnica dei frattali con condensing.
La chioma dell'albero è la seguente:
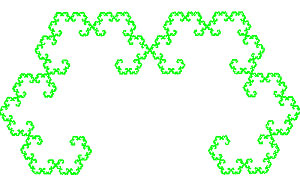
Il risultato ottenuto mostra un altro legame fra frattali e sezione aurea.