Definizioni
Un'omotetia è un tipo particolare di trasformazione affine. Vediamo come è definita.
Consideriamo un punto
O
nel piano ed un numero reale
K
non nullo. La trasformazione
T
che ad ogni punto
A
del piano
fa corrispondere il punto
A'
, allineato con
O
ed
A
e tale che sia :
![]() è detta omotetia di centro
O
e rapporto
K
.
è detta omotetia di centro
O
e rapporto
K
.
La costante K è detta rapporto di omotetia:
- se K >0 l'omotetia si dice diretta,
- se K < l'omotetia si dice inversa.
Possiamo applicare la stessa trasformazione a figure più complesse.
Nell'immagine seguente consideriamo un'omotetia di costante
K=1/2
.
Notiamo che otteniamo una duplicazione della figura di partenza.
Nel caso in cui il centro di omotetia O corrisponda con l'origine degli assi è semplice dare le equazioni analitiche dell'omotetia:
La matrice della trasformazione è la seguente:
Proprietà fondamentali.
Si può dimostrare che un'omotetia gode delle seguenti proprietà:- trasforma una retta in una retta parallela alla retta data;
- l'unico punto unito è il centro di omotetia;
- trasforma una figura geometrica in una figura simile a quella data;
- se la figura S' è l'immagine corrispondente di una figura S, allora Area (S')= K 2 Area (S).
Esempio 1
Consideriamo la seguente omotetia T con centro l'origine degli assi:
![]()
Per capire come agisce T, vediamo come viene trasformato da T il triangolo isoscele ABC (nelle figura 3 in rosso) di vertici A(0,1), B(-1,0), C(0,-1). Il punto A ha come immagine il punto A'(0,2). Il punto B ha come immagine il punto B'(-2,0). Il punto C ha come immagine il punto C'(0,-2).
|
|
|
| (fig. 3) | (fig. 4) |
Notiamo che la figura trasformata (nella figura 4 il triangolo in blu) è un triangolo simile a quello di partenza.
Al posto dei trangoli potremmo considerare qualsiasi tipo di immagine, anche molto più complessa.
Esempio 2.
Consideriamo ora la seguente omotetia
T
di centro l'origine degli
assi:
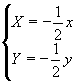
Osserviamo come trasforma la circonferenza di centro il punto di coordinate (1,0) e raggio 1 (fig. 5). La figura trasformata è una circonferenza di centro (-1/2, 0) e raggio 1/2. Si tratta di un'omotetia inversa.
|
|
|
| (fig. 5) | (fig. 6) |